Etudes scientifiques en espaces naturels

Tout traitement informatique ou manuel des données nécessite au préalable de connaître le type de jeu de données que l’on utilise. La première chose à faire est de parcourir les données pour juger de l’importance du travail à effectuer, et découvrir quels types de variables entrent en jeu, quels traitements seront à effectuer. Le poids d’un individu, la couleur des pétales d’une fleur ne sont pas des données de même nature. Il est important de reconnaître les types de  variables car «à chaque variable correspond ses calculs» (voir chapitre 3.2.).

3.1.4.1 Définir la nature des observations

Il est important de considérer la nature des données (observations) que l’on va traiter. Les observations peuvent être soit quantitatives, soit qualitatives.

Variables quantitatives

On désigne par le vocable variable quantitative toute série de chiffres se rapportant à une quantité.

Les données quantitatives comprennent les dénombrements (ou comptages) et les mesures (ou mensurations). Dans le cas des dénombrements, la caractéristique étudiée est une variable discrète ou discontinue, ne pouvant prendre que des valeurs entières non négatives (nombre de pétales par fleur…). Il suffit de compter le nombre d’individus affectés par chacune des valeurs (fréquences) de la variable.

Dans le cas de mesures, la variable est de nature continue (hauteur, poids, surface, concentration, température…). Les valeurs possibles sont illimitées mais du fait des méthodes de mesure et du degré de précision de l’appareil de mesure, les données varient toujours de façon discontinue.

Variables qualitatives

On désigne par le vocable variable qualitative toute série de chiffres se rapportant à des qualités (voir aussi encadré). Les données qualitatives peuvent être assimilées au cas des variables discontinues, en supposant que les différentes variantes du caractère qualitatif sont rangées dans un ordre correspondant par exemple à la suite des nombres entiers positifs (différentes couleurs, différents degrés d’infection…).

3.1.4.2 Caractériser le jeu de données

Photo n°52 : Mesure de la taille du bec d’un Fou de Bassan dans la RN des Sept-Iles. © LPO ÎLE GRANDE.

Ensuite, il faudra chercher à caractériser l’ensemble des données car les traitements statistiques diffèrent d’un jeu de données à l’autre.

Série statistique simple

Une série statistique simple est un ensemble de données relatif à une variable mesurée sur un échantillon ou une population d’éléments (SCHERRER, 1984). Exemple : la taille des individus d’une espèce.

Série statistique double

Une série statistique double est un ensemble de couples de données relatif à la même mesure de deux variables sur un échantillon ou une population d’éléments. Comme ces deux variables peuvent être indifféremment qualitatives ou quantitatives, il est possible de distinguer trois cas de figure :

• les deux variables sont quantitatives. Il s’agit, par exemple, d’une série d’individus dont on mesure la taille et le poids,
• les deux variables sont qualitatives : par exemple le sexe et le comportement d’une série d’individus,
• une variable est qualitative et l’autre quantitative : poids et sexe d’une série d’individus. Par exemple lors d’un suivi d’oiseaux par baguage, on relève sa taille, son poids, la longueur alaire, mais aussi sa provenance (oiseau bagué)…

Série statistique multiple

Le nom de série statistique multiple est réservé aux séries comportant plus de deux variables. Il s’agit donc d’un ensemble de données relatives à la mesure de «p» variables sur un échantillon de «n» éléments ou une population de «N» unités.

3.1.4.3 Construire la matrice des données

Lors de la collecte des données, les valeurs observées se trouvent évidemment sans ordre. Si le volume d’informations devient encombrant, il devient très vite difficile de dégager les caractéristiques ou les faits importants de cette accumulation de chiffres. L’ensemble des résultats bruts acquis et saisis dans la base de données doit être structuré pour faire avancer la compréhension d’un phénomène et réaliser des graphiques (voir chapitre 3.2.1) et des tests statistiques (voir chapitre 3.2.3).

Organiser les données

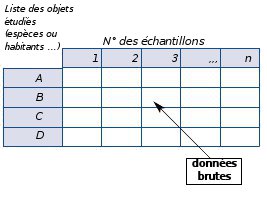Figure n°56 : Modèle général de construction d’une matrice de données.

L’organisation des données dans un tableau sous un format particulier est nécessaire pour le calcul de divers indices ou encore la détermination des associations végétales par le regroupement et la comparaison des données issues de plusieurs relevés (tableaux phytosociologiques de Braun-Blanquet par exemple).

Le gestionnaire procèdera au regroupement ou au classement des observations, dans un tableau à double entrée appelé «matrice des données» (tableau de distribution de fréquence par exemple) à partir duquel il devient possible de les représenter graphiquement. Dans ce tableau, chaque ligne de résultats correspond aux caractéristiques d’un élément, et chaque colonne aux différentes variantes de chacune des variables (voir Figure n°56).

Recommandations

Ces tableaux peuvent être réalisés à l’aide du logiciel Excel, qui permet des analyses croisées de jeux de données (notamment après exportation des données à partir de la base de données servant à la saisie, notamment à l’aide du logiciel SERENA de RNF (voir page 73).

Dans la plupart des cas, il est nécessaire de procéder à un traitement préalable adéquat du tableau initial (codages particuliers…).
Si la fréquence d’observation n’a pas été respectée, il est possible de calculer les données des échantillons manquants (voir encadré ci-contre).
Si l’effectif de l’échantillon est faible, il n’y a pas d’inconvénient à conserver les données les unes à la suite des autres sans les classer.

3.1.4.4 Types de tableaux obtenus

Pour effectuer un tel classement, on distingue les séries statistiques simples des séries statistiques doubles, (voir chapitre 3.1.4.2) (SCHERRER, 1984).
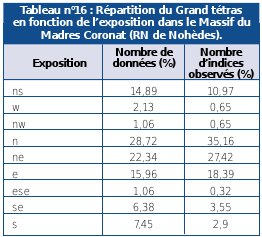
Le cas des séries statistiques simples Dans le cas de séries statistiques simples, on réalise un tableau de distribution de fréquence. C’est un mode synthétique de présentation des données numériques, montrant comment les résultats enregistrés sur une variable se distribuent dans les différentes classes d’une échelle de valeurs ou dans différentes catégories qualitatives (SCHERRER, 1984). Pour préparer un tableau de distribution de fréquence, il faut déterminer des classes et compter le nombre d’éléments appartenant à chacune d’elles (voir Tableau n°16 et n°17). La construction des tableaux de distribution de fréquence nécessite donc le calcul de fréquences.

C’est ce type de tableau qui est obtenu à partir de la plupart des données recueillies dans les réserves naturelles.

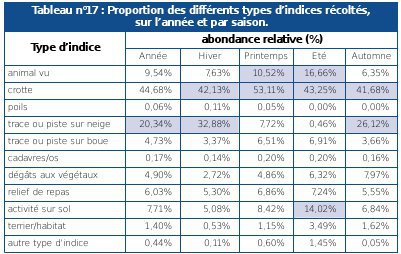Source : LETSCHER, 2001

Dans ce type de tableau, on présentera éventuellement les variables par ordre décroissant. On pourra ainsi faire ressortir un effet de taille (voir Tableau n°24).

Le cas des séries statistiques doubles

Photo n°53 : Accenteur mouchet à la RN de l’Etang de la Mazière. ©  A. DAL MOLIN/L. JOUBERT.

Dans le cas des séries statistiques doubles avec deux variables quantitatives, on réalise un tableau dit de corrélation. Connaissant les bornes de chaque classe sur chacune des variables, on construit un tableau à double entrée portant les indices de classe de la variable x dans le sens horizontal et de la variable y dans le sens vertical. Pour chacune des cellules correspondant aux intersections des lignes et des colonnes, on dénombre les éléments appartenant à cette classe (SCHERRER, 1984).

Si on étudie simultanément deux caractéristiques qualitatives, les résultats sont classés en un tableau de contingence. Dans ce tableau à double entrée, les colonnes correspondent aux différentes catégories de classement de la première variable qualitative, et les lignes aux catégories de classement de la deuxième variable. Dans chacune des cellules coïncidant avec les intersections des colonnes et des lignes, on porte le nombre d’éléments appartenant aux catégories correspondantes (voir Tableau n°18).

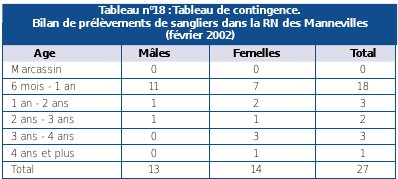Source : Bilan 2002 de la réserve naturelle des Mannevilles.

Les données de séries statistiques doubles avec une variable qualitative, l’autre quantitative, sont elles aussi classées dans un tableau à double entrée, qui résulte de la combinaison d’un tableau de contingence et d’un tableau de corrélation (voir Tableaux n°19 et n°20).

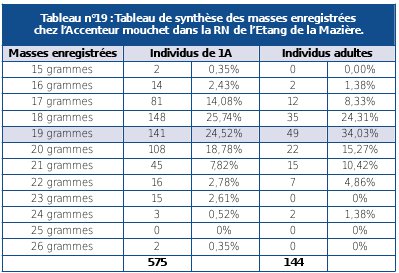Source : DAL MOLIN et al., non daté

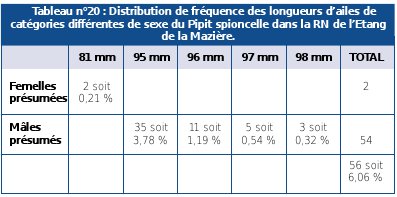Source : DAL MOLIN et al., non daté

Le cas des séries statistiques multiples

Les données issues de séries statistiques multiples qui feront l’objet de représentations graphiques (voir pages 80 et 81) sont elles aussi présentées sous forme matricielle, c’est-à-dire d’un tableau composé de «p» colonnes et de «n» lignes (SCHERRER, 1984) pour permettre une analyse factorielle (voir page 81). Le tableau n°21 est par exemple réalisé à partir du tableau de données brutes n°15.

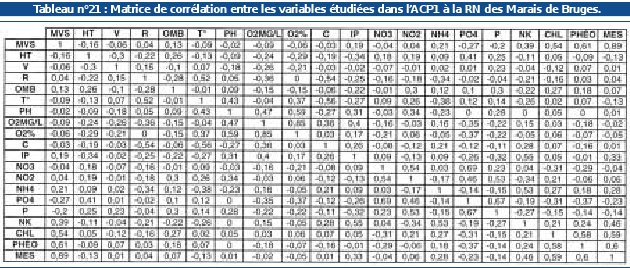Source : MERIGON et al., 1999