3.2.2 - Effectuer le calcul des paramètres de distribution
Il s’agit ici de décrire les séries statistiques. Un paramètre de distribution est une caractéristique quantitative qui permet une représentation condensée de l’information contenue dans une série statistique simple, double ou multiple (voir page 74) obtenus à partir des tableaux de données classées (tableaux n° 16, 17, 18, 19, 20). Ce type de calcul est effectué quand les données se rapportent à un petit nombre de variables mesurées sur un grand nombre d’éléments (échantillons). On distingue les paramètres de position, de dispersion et de totalisation. La première chose à faire, après avoir parcouru les données est de séparer les variables quantitatives et qualitatives, puis de faire toutes les analyses univariées, c’est-à-dire de calculer toutes les moyennes, variances, écarts-types…
Les formules mathématiques des calculs ne sont pas détaillées ici. Le gestionnaire pourra se référer aux références bibliographiques pour en savoir plus, notamment l’ouvrage de biostatistiques de Bruno SCHERRER (1984) ou tout autre ouvrage de statistique.
3.2.2.1 Calcul des paramètres de séries statistiques simples
Pour une variable quantitative :
On indique le nombre de valeurs et on calcule les paramètres de position, les plus utilisés sont la moyenne (m) et la médiane, puis les paramètres de dispersion des variables qui renseignent sur l’étalement de la distribution. En effet, deux distributions peuvent avoir la même moyenne, la même médiane et le même mode et présenter des formes très différentes. Ces paramètres de dispersion sont l’étendue de la variation, la variance (V), l’écart-type (voir Tableau n°23) et le coefficient de variation. Il est également conseillé de fournir la valeur minimale et la valeur maximale.
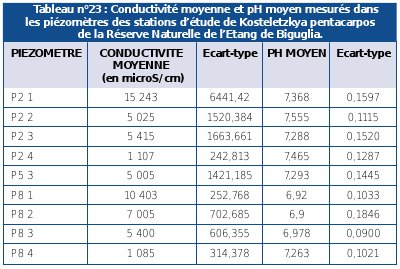 Source : RAVETTO et al., 1997 |
Pour une variable qualitative :
Avec les variables qualitatives un élément n’est pas caractérisé par une mesure quantitative mais par son appartenance à une catégorie définie a priori. Dans ce cas, la distribution de fréquence indique le nombre d’éléments relevant de chacune des catégories (voir Tableau n°19 ou n°20 par exemple). Pour de telles variables, le seul paramètre ayant une signification est le mode, qui correspond à la catégorie la mieux représentée, c’est-à-dire celle qui affiche la plus forte fréquence. Si on considère le tableau n°24, les espèces peuvent être considérées comme les différentes catégories ou réalisations possibles d’une variable qualitative. La catégorie la plus représentée est le Renard roux. Il s’agit donc de la classe modale qui, en écologie, s’appelle l’espèce dominante.
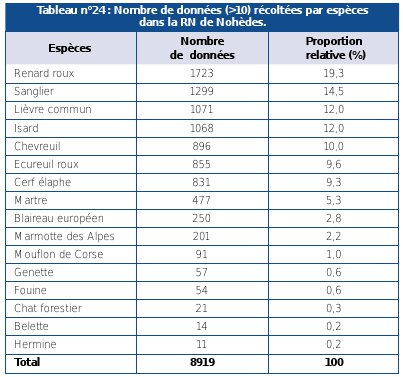 Source : LETSCHER, 2001 |
3.2.2.2 Calcul des paramètres de séries statistiques doubles
3.2.2.3 Calcul des paramètres de séries statistiques multiples
Le centre de gravité est l’extension, à une série bi- ou multidimensionnelle, du concept de moyenne. Il est donc à une série statistique double ou multiple ce que la moyenne est à une série statistique simple. L’écriture matricielle (voir Tableau page 77) est pratiquement toujours utilisée pour représenter les données et les paramètres des séries statistiques multiples. Pour en savoir plus le gestionnaire se réfèrera à la bibliographie.
3.2.2.4 Calcul de l’intervalle de confiance
L’intervalle de confiance est la limite dans lesquelles un paramètre a «x» chances de se trouver. On fait appel à des tables pour trouver les intervalles de confiance. Plus l’intervalle de confiance est grand, meilleure sera l’estimation. L’intervalle de confiance peut être calculé pour la moyenne, la médiane, la variance, l’écart-type.
Dans les espaces naturels on recherchera surtout l’estimation la plus satisfaisante d’un paramètre mesuré sur un certain nombre d’échantillons. Elle devra être exempte de biais et posséder le plus petit intervalle d’incertitude pour le type d’échantillonnage pratiqué.
On pourra citer l’exemple de la RN de la Mazière dans laquelle le gestionnaire a cherché à savoir, par le biais d’une analyse statistique du millier de données enregistrées pendant 3 ans – et réputées homogènes car relevées par deux personnes mesurant exactement de la même manière – s’il était possible de mettre en évidence la détermination présumée du sexe chez le Pipit spioncelle par la seule analyse de la longueur alaire. Les résultats obtenus (fourchette d’incertitude pour trois observateurs) paraissent confirmer cette possibilité (voir Tableau n°25).
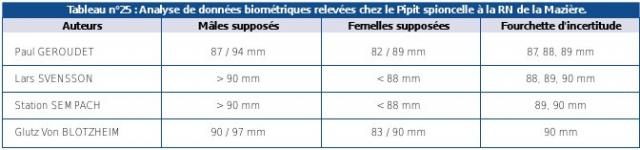 Source : DAL MOLIN et al., non daté |