Etudes scientifiques en espaces naturels

3.2.1.1 Représentation graphique des distributions de série à 1 ou 2 variables

Les données de séries statistiques simples ou multiples relatives à un site peuvent être représentées graphiquement. Les séries statistiques à deux variables qualitatives ne sont généralement pas représentées graphiquement.

Les histogramme (diagramme en bâton)

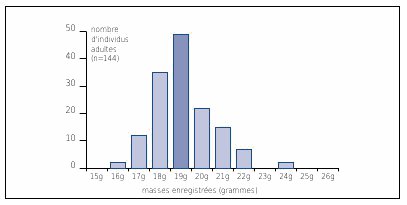Figure n°57 : Histogramme des masses enregistrées chez l’Accenteur mouchet dans la RN de L’Etang de la Mazière. Source : DAL MOLIN et al., non daté

Dans un histogramme, les effectifs des différentes classes sont reportées par des rectangles de hauteurs proportionnelles à chaque effectif. On peut représenter aussi bien des variables qualitatives que quantitatives.
Les données issues du tableau n°16 ou encore du tableau n°19  peuvent être transcrites sous la forme de tels histogrammes (voir Figures n°57 et n°58). Les histogrammes peuvent représenter des effectifs absolus ou bien des pourcentages. On peut 

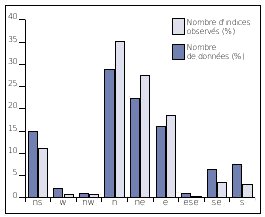Figure n°58 : Histogramme de répartition du Grand tétras en fonction de l’exposition dans le massif du Madres Coronat. Source : MOREAU, 1996

construire le même type de diagramme pour les effectifs cumulés. 

Les polygones de fréquences

Dans ce type de graphique, les indices de classe de la variable sont portés en abscisse et les fréquences en ordonnée. Il convient surtout aux données continues des séries statistiques simples. On peut se représenter les polygones de fréquence par des lignes brisées qui relient les sommets des rectangles dans un histogramme. Le tableau n°19 (synthèse des masses enregistrées chez l’Accenteur mouchet) peut être représenté, par exemple, par un polygone de fréquence (voir Figure n°59).

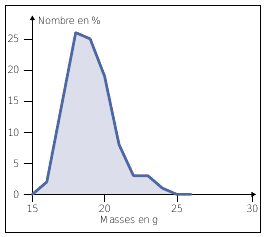Figure n°59 : Polygone de fréquence des masses enregistrées chez l’Accenteur mouchet dans la RN de l’Etang de la Mazière. Source : DAL MOLIN et al., non daté

Attention : ce type de graphique n’a de sens qu’avec des données numériques. Dans le cas de variables qualitatives, on peut au préalable classer les variables par fréquences décroissantes (ou croissantes) avant de réaliser le graphique.

Les diagrammes de dispersion

Ils permettent de représenter des données quantitatives issues de séries statistiques doubles. Ce type de diagramme présente en abscisse la variable «x» et en ordonnée la variable «y» (voir Figure n°60). En plaçant chaque élément dans ce système de coordonnées, on obtient un nuage de points (lorsque les deux variables sont quantitatives).

Les diagrammes en secteurs

Dans un diagramme en secteur (appelé de façon familière «camembert»), les effectifs des différentes classes sont représentés par des secteurs d’angles proportionnels aux effectifs. On s’en sert généralement pour représenter les effectifs de variables qualitatives (voir Figure n°61).

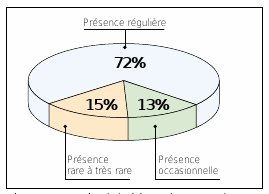Figure n°61 : Graphe général des espèces recensées sur le site de la RN de la Mazière de 1969 à 1994.

Les courbes de fréquence

Les données issues de séries statistiques doubles avec une variable qualitative, l’autre quantitative, sont représentées graphiquement par une série de courbes de fréquence ou d’histogrammes (voir aussi page 78). Chaque courbe ou histogramme se rapporte alors à une catégorie de la variable qualitative. Par exemple, grâce à diverses données calculées (taille moyenne des pieds marqués, écart-type et taux d’accroissement moyen), on peut tracer le graphe des  taux d’accroissement moyen des pieds de l’espèce Kosteletzkya pentacarpos dans 5 stations d’étude à Biguglia (Figure n°62).

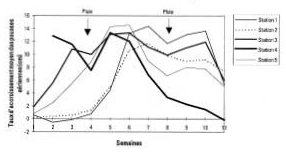Figure n°62 : Taux d’accroissement moyen des pousses aériennes de Kosteletzkia pentacarpos dans cinq stations d’étude de la Réserve Naturelle de l’Etang de Biguglia. Source : RAVETTO et al., 1997

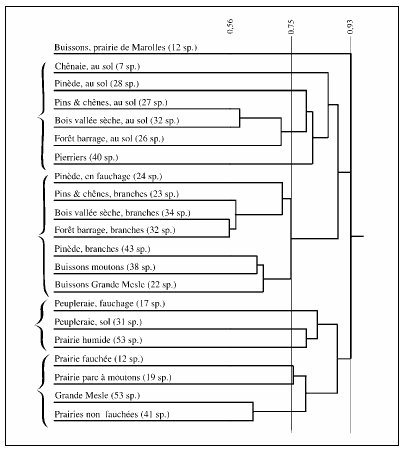
Dendrogrammes

Les dendrogrammes permettent d’illustrer les affinités des variables entre elles. Ces dendrogrammes sont établis à partir du calcul des distances de Jaccard (voir Figure n°63).

Figure n°63 : Affinités entre milieux pour les peuplements aranéologiques dans la RN de Grand Pierre et Vitain. Lors d’une étude du peuplement aranéologique de la RN, les scientifiques ont cherché à savoir quelles sont les affinités entre milieux. Le dendrogramme a été obtenu en calculant les stations par l’indice de Jaccard (I = 1 – c / p + q – C). Où «c» est le nombre d’espèces en commun entre 2 stations ; «p» le nombre d’espèces présentes dans la première station ; «q» le nombre d’espèces présentes dans la deuxième station. Cet indice va de 0 (identité parfaite) à 1 (aucun point commun) par construction ascendante hiérarchique et lien moyen (à chaque étape, le programme recherche la paire de stations dont la distance et la plus faible, puis recalcule les distances entre la paire créée et les autres stations en prenant la moyenne arithmétique des distances). Les milieux rencontrés se répartissent en 3 ensembles : - celuis des pelouses sèches, - celui des forêts, et celui, par certains côtés intermédiaires, constitué par les pairies humides et par la peupleraie. Source : LEDOUX et EMERIT, 2000

3.2.1.2 Représentation graphique de séries statistiques multidimensionnelles (analyses factorielles)

Au travers de techniques de visualisation, les méthodes factorielles permettent de résumer, de structurer et de synthétiser l’information contenue dans des masses volumineuses de données, ceci pour ne garder que les données les plus pertinentes.

Le type d’analyse dépend essentiellement de la nature des paramètres étudiés. Trois méthodes maintenant classiques constituent les outils de base des analyses factorielles. Ces différentes techniques ont des fondements théoriques communs. L’objectif général commun à ces différentes techniques d’analyse factorielle est de représenter de façon synthétique à l’aide de graphiques «l’information» contenue dans un tableau de données. L’idée générale est, à partir d’un tableau de données numériques, voir page 77 («n» lignes, «p» colonnes), de représenter ces données par un nuage de «n» points dans un espace de dimension «p» et par un nuage de «p» points dans un espace de dimension «n».
Il convient de souligner qu’un graphique d’ACP ne se lit pas comme un graphique AFC.

L’analyse en composantes principales (ACP),

Ce type d’analyse traite de tableaux croisant les individus (lignes) et les variables numériques qui caractérisent ces individus (colonnes). L’ACP permet de déterminer les variables principales d’un échantillon. Par exemple la distribution de paramètres physico-chimiques de l’eau permet de distinguer des groupes de variables (voir Figure n°64).

Figure n°64 : Analyse en Composantes Principales portant sur les paramètres physiques et physico-chimiques ainsi que sur les différents taxons répertoriés sur chacune des stations, dans le cadre d’une étude sur la qualité de l’eau dans la RN des Marais de Bruges. Source : MERIGON et al., 1999 Dans un premier temps les taxons ont été codés à l’aide de 4 lettres. Cet ACP permet de distinguer grossièrement 5 groupes : - L’ombre portée (O), la vitesse du courant (V), et le pH (PH) contribuent à l’axe 1 et semblent aller dans le même sens. Il en est de même pour certaines espèces de macrophytes aquatiques telles que Solanum dulcamara (SOLD), Glyceria maxima (GLYM), des ronces (RUBX), des orties (URTX), des algues filamenteuses (ALGF) et des graminées (GRAM). - La turbidité (TU), l’épaisseur du substrat (HS), le genre Lemna (LEMX) et le genre Juncus (JUNX) contribuent aussi à l’axe 1 mais semblent être corrélés négativement avec le groupe précédent. - Le troisième groupe est formé par les variables H (hauteur d’eau), SPAR (sparganium erectum), RICF (Riccia fluitans), WOLA (Wolffia arrhiza) et LEMP (Lemna polyrhiza) et contribue à l’axe 2. - PLGH (Polygonum hydropiper), CERD (Ceratophyllum demersum), CLYX (Calystegia sp.), RANX (Ranunculus sp.), LEMT (Lemna trisulca), RORA (Rorippa amphibia), CALX (Callitriche sp.), T (température), 02 (Oxygène dissous) et O2% (taux de saturation de l’oxygène dissous) contribuent également à l’axe 2 mais semblent ne pas aller dans le même sens que le groupe précédent. - IRIP (Iris pseudacorus) contribue à la fois aux axes 1 et 2. Extrait de MERIGNON et al., 1999

L’analyse factorielle des correspondances (AFC)

Ce type d’analyse traite des tableaux de fréquence, et de ce point de vue on peut considérer en première approche que c’est un mode de représentation graphique des tris croisés multiples. Les données récoltées dans la RN de Nohèdes et issues de l’analyse croisée entre mammifères et expositions permettent de réaliser une AFC (voir Figure n°65).

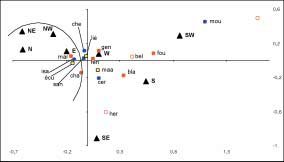Figure n°65 : Relation entre espèces de mammifères et expositions dans la RN de Nohèdes. Analyse Factorielle des Correspondances à Variables Instrumentales. Axes 1-3. Source : LETSCHER, 2001

C’est la méthode d’analyse numérique la plus fréquemment employée, notamment dans les réserves naturelles. Elle est particulièrement bien adaptée à l’analyse des variables qualitatives et aux tableaux de données quantitatives, si les valeurs du tableau sont positives. Elle permet de comparer des variables qualitatives entre elles et fait ressortir les différences relatives entre les variables. C’est une technique statistique très bien adaptée aux analyses phytosociologiques d’ordination des relevés et donc des groupements végétaux (GUINOCHET, 1973).

L’analyse des correspondances multiples (ACM).

Photo n°55 : Kosteletzkya pentacarpos, une espèce végétale étudiée dans la RN de l’Étang de Biguglia © S. RAVETTO/RN ÉTANG DE BIGUGLIA

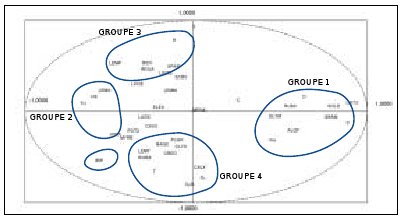
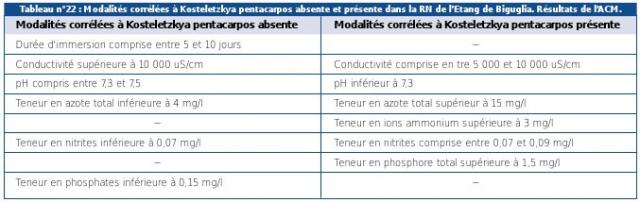
Ce type d’analyse s’applique à des tableaux de valeurs codifiées. Par exemple, pour mesurer l’influence des paramètres de la nappe sur la répartition de Kosteletzkya pentacarpos dans la RN de l’Etang de Biguglia, une ACM a été réalisée. Dix variables sont choisies dont neuf quantitatives (durée de l’immersion du milieu, pH de l’eau, conductivité de l’eau, teneur en azote total, ions ammonium, nitrites, nitrates, phosphore total, phosphates) et une qualitative (la  présence de l’espèce).

Chaque variable a été divisée (codifiée) en plusieurs modalités (au moins deux) qui diffèrent selon les stations. Pour les variables quantitatives, ces modalités sont les classes de valeurs (par exemple «NH4b» pour NH4 < 3 mg/l, «Di a» pour Durée d’immersion < 5 jours) tandis que pour les variables qualitatives ces modalités sont : absente, rare, présente ou abondante. On obtient ainsi un graphique (voir Figure n°66).

Figure n°66 : Regroupement des différentes modalités pour l’ACM sur les différents paramètres de la nappe dans la zone d’étude de Kosteletzkya pentacarpos au sud de l’étang de Biguglia. Source : RAVETTO et al., 1997

A partir du graphique précédent (Figure n°66), il est possible de corréler la présence ou l’absence de l’espèce étudiée en fonction des modalités du milieu (voir Tableau n°22) Source : RAVETTO et al., 1997